우리가 흔히 하는 PC나 게임기로 즐기는 비디오 게임은 다양한 곳에서 재미를 위해 AI를 활용합니다. 1인용 게임에서 플레이어를 지원하는 AI, 스테이지 전략이나 적의 출현을 조절해서 게임 분위기가 뜨거워지도록 만드는 메타 AI, 대전 격투 게임에서 인간 대신에 대결 상대가 되어주는 대결 AI 등, 게임에 도입된 AI 용도는 상당히 다양합니다.

이중에서 특히나 대결 AI에서는 탐색 기술을 많이 사용합니다.
게임을 플레이하는 AI라고 하면 자주 등장하는 이름이 있습니다. 바로 구글의 딥 마인드DeepMind가 개발한 알파고AlphaGo입니다. 2015년부터 2017년까지 펼쳐진 당시 최정상 바둑 기사들과 알파고의 대결은 엄청난 충격을 몰고 와서 수많은 미디어와 뉴스에서 다루어졌습니다. 바둑 AI가 인류를 뛰어넘는 건 아직 먼 훗날이라고 말하던 때였고 그 당시 아직 널리 알려지지 않았던 딥러닝deep learning을 사용했기 때문에, 게임 AI는 딥러닝처럼 뭔가 엄청난 기술을 사용하는 것이라고 느끼신 분도 많을 것입니다.
딥러닝은 넓게 보면 머신러닝 분야의 기술입니다. 대전 게임 AI는 이런 머신러닝뿐만 아니라 규칙 기반, 탐색, 이런 세 종류의 기술 요소를 사용합니다. 이중에서 규칙 기반은 사람이 직접 만든 규칙에 따라 조건 분기하는 것을 뜻합니다. 이번에는 탐색에 중점을 두고 이야기하고자 합니다.
책 <게임 AI를 위한 탐색 알고리즘 입문>에서는 조합론적 게임 이론의 게임 트리game tree 탐색과 조합 최적화를 사용한 메타 휴리스틱metaheuristic을 포함해서 탐색이라고 부릅니다. 조합론적 게임 이론에서는 게임의 진행을 유향 그래프로 표현하고, 게임판을 노드node, 수(선택지)를 엣지edge로 표현한 것을 게임 트리라고 부릅니다.
갑자기 전문 용어가 잔뜩 등장해서 어려워졌네요. OX 게임을 예를 들어 설명해 보겠습니다.
OX 게임은 2명의 플레이어가 교대로 순서가 되면 돌을 두는 게임입니다. 가로, 세로 3칸짜리 판에 O와 X 말을 번갈아 두면서 자신의 말이 가로, 세로, 대각선 어느 방향이든 연달아 3개가 모이면 이깁니다. 학창 시절에 모눈종이 위에 했던 오목 게임과 비슷합니다. 시작 후 4턴이 지난 게임을 함께 살펴봅시다. 이때 X가 선공입니다.
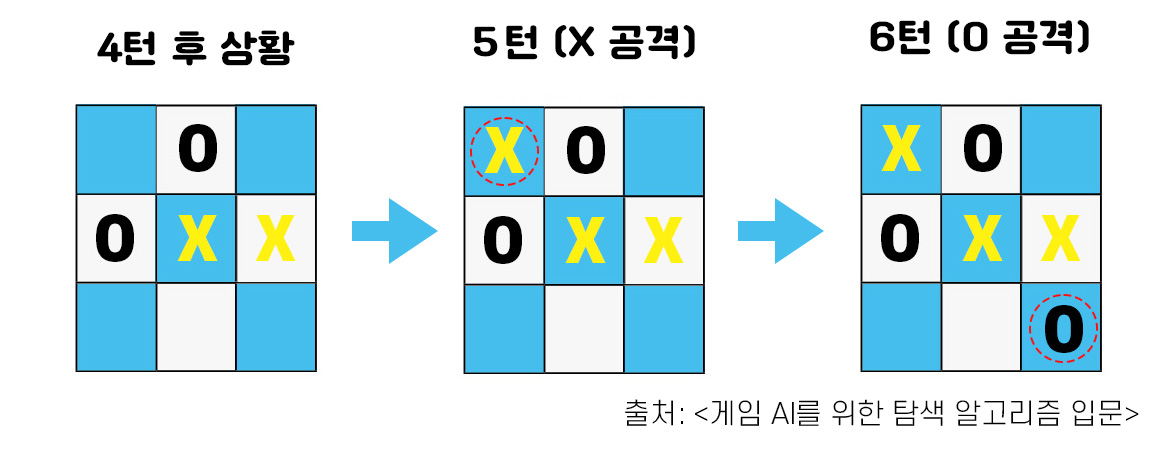
5턴에서 X쪽 플레이어가 왼쪽 위에 X를 두었습니다. 이러면 대각선 방향으로 리치*가 됩니다. 하지만 이대로 끝나지 않을 것 같습니다. 6턴째에 공격을 하는 O쪽 플레이어가 오른쪽 아래에 O를 둬서 X쪽 플레이어의 공격을 방어할 수 있기 때문입니다 . X쪽 플레이어 입장에서는 왼쪽 위에 X를 둔 건 실패라고 볼 수 있죠.
*리치: 일본 마작에서 온 용어로, 우노 카드 게임에서 카드가 한 장 남으면 우노라고 외치는 것처럼 곧 게임이 끝난다고 알리는 말입니다. 즉, 게임이 끝날 때까지 하나 남았다는 상황을 뜻합니다.
그럼 X쪽 플레이어는 이길 방법이 없을까요? 아닙니다. 다시 4턴 후 상황으로 돌아가 X쪽 플레이어가 다르게 행동한다면 어떻게 될지 생각해 봅시다.
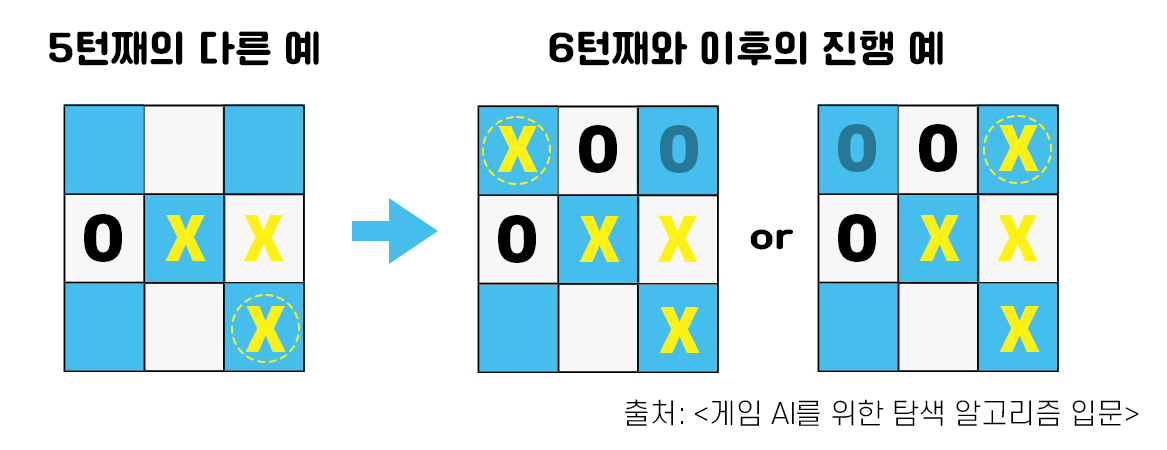
이번에는 5턴째에 X쪽 플레이어가 오른쪽 아래에 말을 두었습니다. 이러면 O쪽 플레이어가 오른쪽 위에 O를 두더라도 다음 턴에 왼쪽 위에 X를 둔 플레이어가 이길 수 있습니다.이렇게 앞으로 펼쳐질 플레이어 행동을 몇 가지 패턴으로 미리 예상하면서 각 플레이어는 자신이 유리한 상황으로 게임을 유도할 수 있습니다.
미래의 상황은 플레이어 행동(수)에 따라 다양하게 갈라지는데 그런 국면을 나열해 보겠습니다. 점(노드) 집합을 선(엣지) 집합으로 연결해서 구성한 것을 그래프 graph라고 하고, 엣지에 방향성이 있으면 유향 그래프 directed graph라고 부릅니다. 그리고 앞서 설명한 것처럼 게임에서 플레이어가 둔 수를 엣지, 게임판을 노드로 나타낸 유향 그래프를 게임 트리라 고 부릅니다.
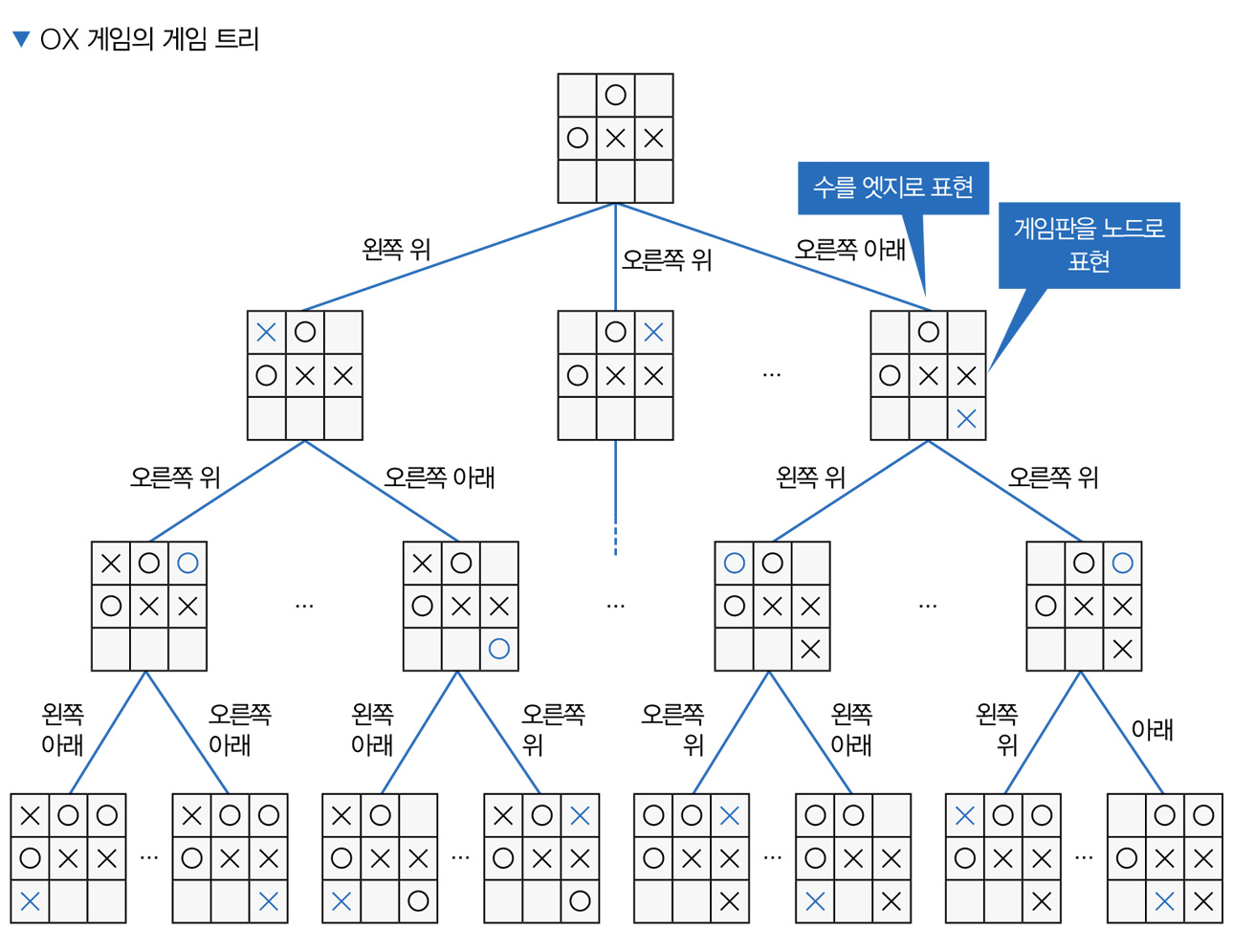
게임의 시작부터 끝까지 모든 수를 포함한 게임 트리를 특별히 완전 게임 트리 complete game tree라고 합니다. 완전 게임 트리를 분석한 플레이어는 언제나 최선의 수를 선택할 수 있습니다. 하지만 게임 트리는 게임 복잡성에 따라 지수 함수적으로 커지고, 한 수를 두는 데 많은 시간을 쓸 수 없기 때문에 대부분의 게임을 완전 게임 트리 분석하는 건 비현실적입니다.
따라서 게임의 일부만 게임 트리로 표현하고, 한정된 자원으로 우선 순위를 정하고 고심 해서 좋은 답을 찾습니다. 이런 기법을 통틀어서 게임 트리 탐색이라고 부릅니다.
게임과 탐색을 설명하는 글에서 자주 보이는 용어가 ‘2인 제로섬 유한 확장 완전정보 게임’입니다. 이건 이름처럼 ‘2인’, ‘제로섬’, ‘유한’, ‘확정’, ‘완전정보’ 이렇게 다섯 가지 특성을 모두 갖춘 게임의 총칭입니다. 2인 제로섬 유한 확정 완전정보 게임에서 완전 게임 트리를 만들면 나중에 설명하는 미니 맥스MiniMax 알고리즘으로 게임을 완전히 분석할 수 있습니다. 2인 제로섬 유한 확정 완전정보 게임의 예에는 장기, 바둑, 오셀로 같은 전통적인 보드 게임이 있습니다. 앞에서 설명한 OX 게임도 이런 종류의 게임입니다.
그런데 장기에는 천일수 규칙(동일 국면이 반복될 경우, 해당 판을 무효로 하고 다시 두는 규칙)이 있어서 이 규칙에 따라 처음부터 다시 두는 경우도 존재합니다. 따라서 장기는 엄밀하게 따지면 유한하지 않고 제로섬도 아니라는 의견도 존재합니다. 물론 바둑도 서로 합의하지 않으면 영원히 끝나지 않는 상황이 존재하므로 유한하지 않습니다. 또한 비디오 게임 등에서는 초보자도 즐길 수 있도록 무작위성을 추가하거나, 정보를 일부러 숨기는 등 예상하지 못한 즐거움을 더하는 경우도 많습니다.
앞서 나열한 다섯 종류 요소 중에서 제로섬, 유한, 확정, 완전정보 요소를 만족하면 할수록 탐색이 쉬워지고 성능도 보장됩니다. 하지만 이러한 요소를 모두 갖춘 게임은 그
다지 많지 않습니다. 따라서 책 <게임 AI를 위한 탐색 알고리즘 입문>에서는 실용성을 따져서 게임을 다음과 같은 관점으로 분류합니다.
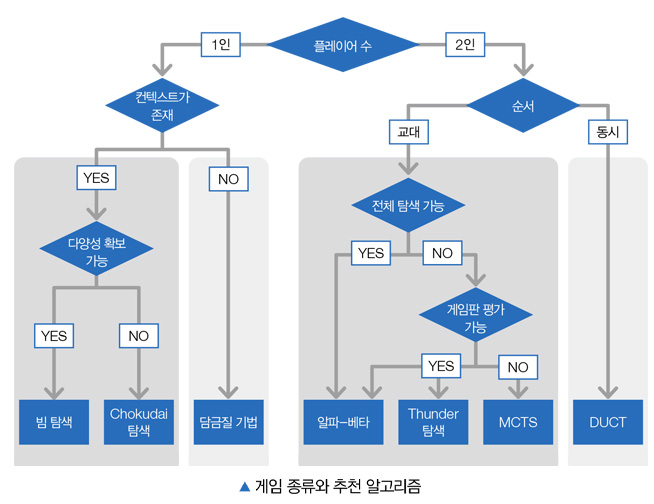
책 <게임 AI를 위한 탐색 알고리즘 입문>에서는 플레이어 수, 컨텍스트 존재 유무, 플레이 진행 순서 등에 따라 크게 네 종류의 게임으로 구분합니다. 이런 네 종류의 게임은 다시 세부 조건을 확인해 빔 탐색, Chokudai 탐색, 담금질 기법, 미니맥스 알고리즘, 알파-베타 가지치기, Thunder 탐색, 순수 몬테카를로 탐색, MCTS 몬테카를로 트리 탐색, DUCT (Decoupled Upper Confidence Tree) 등 다양한 알고리즘을 사용해 게이머에게 더욱 재미있는 게임을 제공할 수 있습니다.
위 내용은 『게임 AI를 위한 탐색 알고리즘 입문』에서 발췌하여 정리하였습니다.
게임 AI 기술 요소는 크게 규칙, 탐색, 머신러닝으로 나뉘며 머신러닝만으로는 먼 미래의 상황을 정확히 읽어내기 어렵습니다. 특히 탐색 기술이 없었다면 강력한 AI는 탄생하지 못했을 겁니다. 물론 실무에서 주어진 요구 사항이나 제한 사항을 해결하기 위해서도 사용되죠. 이러한 탐색 기술의 중요성과 매력은 아래 도서에서 더욱 자세히 확인할 수 있습니다.

이전 글 : 실무에 인과추론 적용하기 위한 험난한 5단계 여정
다음 글 : 게임 AI와 탐색: 탐색 알고리즘의 매력
최신 콘텐츠