[도서리뷰] 알고리즘 인사이드 with 파이썬
알고리즘 인사이드 with 파이썬
알고리즘(Algorithm) 이라고 하면 우선 겁이 나고 어렵다는 생각이 듭니다. 하지만 이 책은 그런 부분을 자세한 설명와 예시를 통해 스스로 학습하고 훈련할 수 있도록 구성되어 있습니다. 먼저, 알고리즘에 기본이 되는 문법에 대해 설명을 해주고,이후 심화 알고리즘과 문제 풀이 등이 담겨 있습니다. 총 86개의 알고리즘 문제를 제공해 주고 있습니다. 이 책의 목적은 보다 많은 개발자가 빠르고 안정적으로 효율적인 알고리즘을 개발할 수 있는 역량을 갖추도록 돕는 것입니다.
이 책의 구성은 LESSON 부분(파트 1, 2)과 PRACTICE 부분(파트 3, 4)으로 나눠져 있고, 파트1은 파이썬 문법, 핵심만 뽑기, 파트 2는 기본 자료구조와 알고리즘, 파트 3은 알고리즘별 문제 풀이 I, 파트 4은 알고리즘별 문제풀이 II, 부록으로 구성되어 있습니다.
PART 01 파이썬 문법, 핵심만 뽑아보기
파이썬은 데이터 처리와 기계학습부터 웹 서버 개발에 이르기까지 다양한 분야에서 널리 사용되는 개발 언어입니다. 특히 파이썬은 간결한 문법과 강력한 내장 자료구조는 알고리즘을 구현할 때 진가를 발휘합니다. 이 책에서 다루는 모든 알고리즘 문제는 파이썬으로 구현했습니다. 따라서 본격적으로 들어가기 앞서 자료구조와 알고리즘을 이해하는 데 필요한 파이썬 핵심 문법과 정규표현식을 알아봅니다.
Chapter 1 파이썬 기본 문법
파이썬은 간결한 작성 방법과 폭넓은 활용 법위로 가장 사랑받는 개발 언어입니다. 알고리즘을 살펴보기 앞서 파이썬에서 꼭 알아 두어야 할 핵심 문법을 살펴보겠습니다. 그중에서도 이번 챕터에서는 기본 문법은 데이터 타입, 반복문 클래스 그리고 멀티 프로세싱에 대해 살펴봅니다.
기본 타입이란? 언어에서 기본으로 제공하는 데이터 타입을 말하며, 사용자가 정의할 필요 없이 바로 사용할 수 있습니다. 대표적으로 숫자형, 문자열 등이 기본 타입에 해당합니다.
숫자형 : 숫자형 데이터 타입은 말 그래도 정수와 실수를 가리키며, 연산이 가능합니다.
문자열 : 파이썬은 문자열과 문자를 구분하지 않습니다. 따라서 큰 따옴표(“)나 작은 따옴표(‘) 중 무엇을 사용해도 문자열을 할당할 수 있습니다.
빌트인 타입
빌트인 타입이란? 리스트, 튜플, 딕셔너리, 집합 등 파이썬에서 기본으로 제공하는 자료구조를 뜻합니다. 알고리즘 구현에 많이 활용하는 타입이므로 반드시 알아 두는 것이 좋습니다.
리스트 : 리스트는 여러 원소를 담은 데이터 타입으로, 변수에 [ ] 또는 list를 대입해 선언할 수 있습니다.
튜플 : 튜플은 리스트와 마찬가지로 여러 값을 하나로 묶는 데이터 타입으로, 선언하는 방법은 2가지 있습니다. 괄호 사이에 1개 이상의 원소를 지정하거나 괄호 없이 값만 입력한 다음 마지막에 콤마(,)를 입력하면 됩니다.
딕셔너리 : 파이썬은 맵 타입의 자료구조로 딕셔너리를 제공합니다. 딕셔너리는 키와 값을 하나의 쌍으로 저장하는 자료 구조로, { } 또는 dict를 사용해 선언할 수 있습니다.
집합 : 집합은 중복을 허용하지 않은 원소 모음을 표현하는 자료구조입니다. 따라서 집합을 선언할 때 중복된 값은 모두 제거하고 저장하는 것을 확인할 수 있습니다. 집합은 { }에 원소를 넣어 선언합니다.
조건문과 반복문
if 문 : 파이썬에서 조건문 if문은 타 언어와 달리 if문 뒤에 괄호를 열지 않고 표현식을 작성해도 코드가 작동합니다. 단, 표현식의 마지막에는 반드시 콜론(;)이 있어야 합니다.
for 문 : for 문은 실행문을 반복하는 반복문으로, range 안에 반복의 시작과 끝 그리고 증감하는 값을 지정해서 실행합니다.
while 문 : for 문 대신 반복문을 구현하는 또 다른 방법은 while 문을 사용하는 것입니다. while 문은 for 문보다 표현식이 복잡할 때 사용합니다.
함수와 람다 표현식
함수 : 파이썬에서 함수를 선언하는 방법은 간단합니다. def로 함수를 정의합니다.
람다 : 파이썬은 익명 함수인 람다 표현식도 지원합니다. 람다 표현식은 func 라는 변수에 할당해 일반 함수처럼 사용할 수 있습니다.
고급 제어
반복자 : 클래스를 반복 가능한 객체로 만들어 반복자로 사용할 수 있습니다. 방법은 간단합니다. 클래스를 정의할 때 __iter__와 __next__ 메서드를 구현하면 됩니다.
제너레이터 : 제너레이터는 yield 키워드를 사용해 호출자에 값을 전달하는 객체로, get_line 함수에서 lines에 있는 값을 하나씩 읽어 들여 호출자로 전달하는 기능을 수행합니다.
데커레이터 : 디자인 패턴에서 기능을 덧붙이는 것을 가르키는 용어로 함수에 기능을 추가할 수 있습니다. 타 언에서는 클래스를 정의하고 상속하는 과정이 필요하지만, 파이썬은 간단히 @로 기능을 추가할 수 있습니다.
코루틴 : 코루틴은 문법적으로 제너레이터와 다르지 않습니다. 차이점이 있다면 2개 이상의 제너레이터가 서로 값을 주고 받으면서 교차 실행된다는 점입니다. 즉 ‘코루틴’이라는 이름처럼 2개 이상의 루틴이 함께 실행된다는 뜻입니다.
클래스
객체 지향 프로그래밍에서 지원하는 클래스를 파이썬에서도 지원합니다. 클래스는 서로 응집되어 하나의 역할을 수행하는 데 필요한 모든 메서드와 속성을 은닉시켜 추상화된 데이터 타입등을 활용 할 수 있습니다.
정적 메서드 : 정적 메서드는 클래스 인스턴스를 생성하지 않고 바로 사용할 수 있는 메서드로, 멤버 속성 등에 접근할 수 없는 순수 함수로 사용합니다.
상속 : 객체 지향의 핵심 개념 중 하나가 상속입니다. 부모가 되는 클래스의 속성과 기능을 기반으로 새로운 클래스를 정의하는 기법입니다.
멀티 프로세싱
파이썬에서 멀티스레딩은 오직 하나의 코어만 사용합니다. 즉, 여러 코어를 사용해 스레드를 병렬로 동작하지 않습니다. 오직 병행 처리만 가능합니다. 이러한 제약이 발생하는 원인은 GIL에 있습니다.
Chapter 2 정규표현식
현재는 파이썬, 자바, GO 등 많은 프로그래밍 언어가 다양한 문법을 제공하지만, 과거 최초의 컴퓨터인 튜링 머신이 탄생할 즈음 컴퓨터 언어는 수학 수식으로만 존재했습니다. 이때 사용했던 언어가 정규 언어입니다. 정규표현식은 바로 이 정규 언어에서 유래되었습니다. 정규표현식은 다양한 패턴을 통해 많은 것을 표현할 수 있고 반대로 패턴을 찾을 수 있다는 장점이 있습니다.
search, match
search 함수는 이름 그대로 원하는 패턴을 찾아 주는 함수입니다. search 함수의 첫 번째 인수에 찾고자 하는 문자 패턴을 입력하고, 두 번째 인수에 찾으려는 대상 문자열을 입력합니다. match 함수는 원하는 문자열을 찾는 코드입니다. 결과는 search 함수를 사용한 것과 동일하지만, match 함수는 찾고자 하는 문자열 패턴 앞에 다른 문자 혹은 공백이 붙어 있으면 이를 찾지 못합니다.
compile
특정 패턴을 반복해야 할 때는 re.compile로 정규표현식의 패턴을 컴파일된 객체로 사용하는 방법이 있습니다. 패턴 뒤에 + 혹은 *, ? 등을 붙이면 패턴이 몇 번 반복되어야 검색을 수행할 것인지에 대한 반복 조건을 지정할 수 있습니다.
findall과 finditer
하나 이상의 대상을 검색하고 싶다면 search나 match가 아닌 findall 혹은 finditer를 사용합니다.
PART 02 기본 자료구조와 알고리즘
알고리즘을 구현하기 위해서는 여러 가지 다양한 자료구조를 응용하여 문제 해결 과정에 적용해야 합니다. 또한 기본적으로 많이 사용하는 알고리즘을 미리 알고 있어야 풀 수 있는 문제가 그만큼 많아집니다. 기본적인 알고리즘은 스택, 큐, 트리, 해시, 그래프를 살펴보고 이어서 검색 및 정렬 그리고 마지막으로 우선순위 큐, Radix 트리 등에 대해 알아보겠습니다.
Chapter 3 핵심 자료구조
스택(Stack)
스택을 저장하는 자료구조는 여러 가지가 있지만 그중 가장 간단하고 흔히 쓰이는 자료구조가 스택입니다. 스택은 대표적인 후입선출(LIFO)로 가장 나중에 들어간 자료가 가장 먼저 출력되는 자료 구조입니다. 스택 자료구조는 push, pop, top, size, empty 등의 기능을 제공합니다.
큐(Queue)
큐는 손님이 들어온 순서대로 처리하는 것을 보장합니다. 즉, 먼저 들어온 손님을 먼저 맞이하고 나중에 들어온 손님은 들어온 소님의 업무 처리가 끝나야 차례가 됩니다. 이렇게 먼저 들어온 손님이 먼저 처리되는, 즉 큐에서 나가는 것을 보장하는 방식을 선입선출(FIFO)라고 합니다. 큐 자료구조는 enqueue, size, dequeue 등의 기능을 제공합니다.
원형 큐(Circular Queue)
큐는 구현방식에 따라 크게 2가지가 있습니다. 선입 선출을 보장하기 위해 선형 방식으로 큐를 운영하는 원형 큐, 순환 큐가 있고 원소의 개수에 따라 큐의 크기가 달라지는 가변 크기 규가 있습니다. 가변크기 큐는 보통 연결 리스트로 구현합니다.
연결 리스트(Linked List)
연결 리스트는 원소가 없으면 0, 원소를 추가하는 만큼 크기가 커지는 것이 특징입니다. 연결 리스트로 큐를 구현하면 연결 리스트의 크기를 자유롭게 변경할 수 있고, 버퍼도 원소가 없으면 0개, 원소가 n개 들어오면 n개로 관리합니다. 연결 리스트는 단일 연결 리스트와 이중 연결 리스트 2가지 종류가 있습니다.
해시(Hash), 맵(Map)
해시, 맵은 특정 값을 추가, 삭제, 검색하는 속도를 높이는 자료구조입니다. 해시는 해시 셋과 해시 맵으로 나뉩니다. 해시 셋은 이름 그대로 집합의 성격을 가지고 있어 중복을 허용하지 않고, 해시 맵으로 구현할 수 있습니다. 해시 테이블이라고 불리는 해시 맵은 추가, 삭제, 검색을 거의 O(1) 속도로 무척 빠르게 수행하는 자료구조입니다. 이는 배열과 리스트의 특징을 모두 갖고 있어 구현도 무척 쉽다는 특징이 있습니다.
트리(Tree)
트리는 하나의 뿌리에서 수많은 가지로 뻗어나가는 모양으로 한 곳에서 여러 형태로 파생되는 계층적 구조를 시각화하는데 사용됩니다. 트리 형태로 흔히 표현하는 것 중에 하나가 가족 관계를 나타내는 가계도입니다. 대표적 트리로 이진트리가 있습니다.
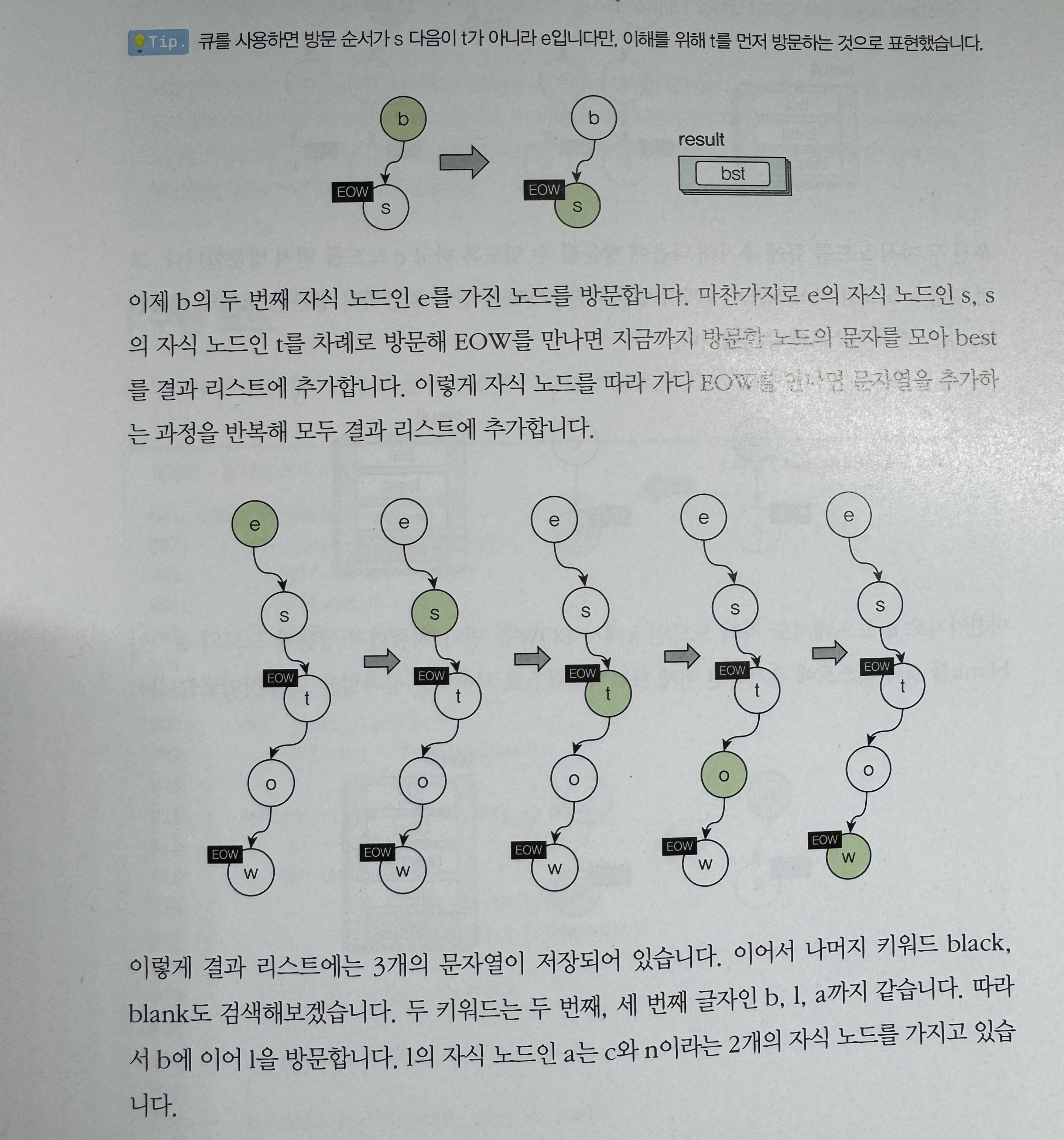
트라이(Trie)
트리의 한 종류로 prefix tree라고 합니다. 앞서 살펴본 이진 트리와 달리 자식 노드의 개수에 제한이 없고 키값의 대소 관계를 파악하여 값을 찾는 것이 목적이 아니므로 노드를 추가할 때 키값의 크기에 따라 노드의 위치를 고려할 필요가 없습니다. 트라이는 보통 문자 혹은 문자열을 저장하고 이를 빠르게 검색하는 용도로 사용합니다.
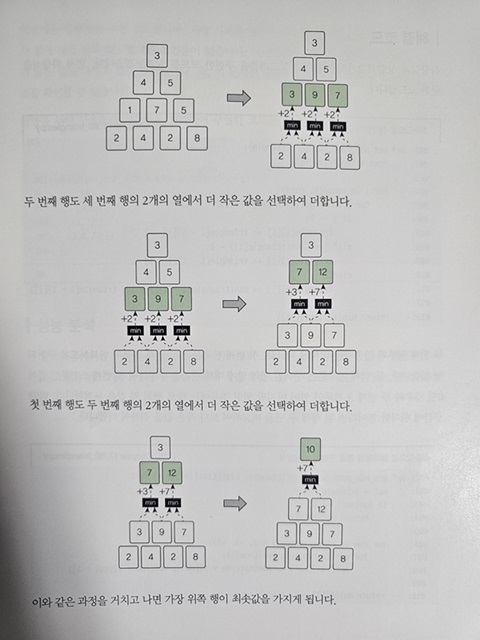
힙(Heap)
큐는 선입선출방식으로 데이터를 처리하는 대표적 자료구조입니다. 우선순위 큐는 최솟값을 기준으로 큐에서 값을 내보내는 자료구조로, 내부에서 연결 리스트를 사용하거나 트리를 이용해 구현할 수 있습니다. 그러나 연결 리스트로 구현하면 자료구조의 특성 때문에 성능이 그리 좋지 않습니다. 가장 성능 좋은 우선순위 큐를 구현할 때는 힙이라는 자료구조를 사용합니다. 힙은 루트 노드가 항상 가장 작은 값임을 보장하는 자료구조이기 때문에 힙으로 우선순위 큐를 구현하면 가장 작은 값의 검색을 O(1)의 시간 복잡도로 수행할 수 있습니다. 그렇기에 힙 자료구조를 사용하여 구현한 우선순위 큐가 최솟값을 획득할 때 가장 성능이 좋습니다.
그래프(Graph)
관계성을 시각적으로 쉽게 표현하는 방법이 그래프입니다. 그래프는 정점과 간선으로 구성됩니다. 정점은 그래프의 구성 요소를 의미합니다. 간선은 정점과 정점의 관계, 즉 ‘관련이 있음’을 표현합니다. 여러 개의 정점과 간선이 모여 그래프를 형성합니다. 그래프는 정점 간 방향성이 있느냐 없느냐에 따라 유향 그래프와 무향 그래프로 나눌 수 있습니다. 방향과 상관없이 간선에 가중치를 두는 가중치 그래프도 있습니다. 가중치 그래프란, 어떤 한 정점에서 연결된 다른 정점으로 이동할 때 얼마만큼의 비용이 소모되는지를 표시한 그래프입니다. 최단 거리, 공정 문제 등 다양한 분야에서 간선의 가중치를 활용하여 문제를 해결할 수 있습니다.
Chapter 4 기본 알고리즘
정렬
정렬은 특정 기준에 맞춰 값을 나열하는 과정입니다. 가장 흔히 볼 수 있는 예로는 오름차순/내림차순 정렬이 있습니다. 이외에도 값이 생성된 시간이나 출현하는 순서에 따라 나열하는 등 다양한 정렬이 있습니다. 정렬 방식에 따라 성능이 달라지기도 합니다. 가장 성능이 좋은 정렬은 사실 퀵 정렬이며, 퀵 정렬은 분할 방식을 사용해 실제 실행 시간의 성능을 높일 수 있기 때문입니다.
구현이 단순한 정렬 : 버블 정렬, 선택 정렬, 삽입 절열, 셀 정렬
구현이 복잡한 정렬 : 힙 정렬, 병합 정렬, 퀵 정렬, 기수 정렬
그래프 알고리즘
그래프에서 살펴본 인접 행렬, 인접 리스트, 셋 등으로 그래프의 구성 요소와 구현 형태 등을 살펴봤다면, 이번에는 기본적인 탐색 알고리즘인 깊이 우선 탐색, 너비 우선 탐색을 시작으로 최단 경로 구하기, 모든 노드를 최소 비용으로 연결하기, 순서를 보장하는 위상 정렬 등을 살펴봅니다.
문자열 검색
문자열 검색이란 말 그대로 문자열로 주어진 문자 배열에서 원하는 패턴의 배열을 찾는 것입니다. 문자열을 검색하는 가장 흔한 방법은, 문자열의 길이가 M이고 찾고자 하는 부분 문자열의 길이가 N 이라고 할 때 O(MN)의 시간 복잡도를 찾는 것입니다. 그러나 KMP 알고리즘 그리고 라빈-카프 알고리즘 등은 문자열 검색을 O(N)의 시간 복잡도로 수행할 수 있습니다.
PART 03 알고리즘별 문제 풀이 I
개발자라면 반드시 알아야 하고 문제 해결 능력을 증진시키는 데 도움이 되는 핵심 알고리즘(재귀, 탐색, 공간, 순열과 조합, 배열, 정렬, 검색, 문자열)을 다룹니다.
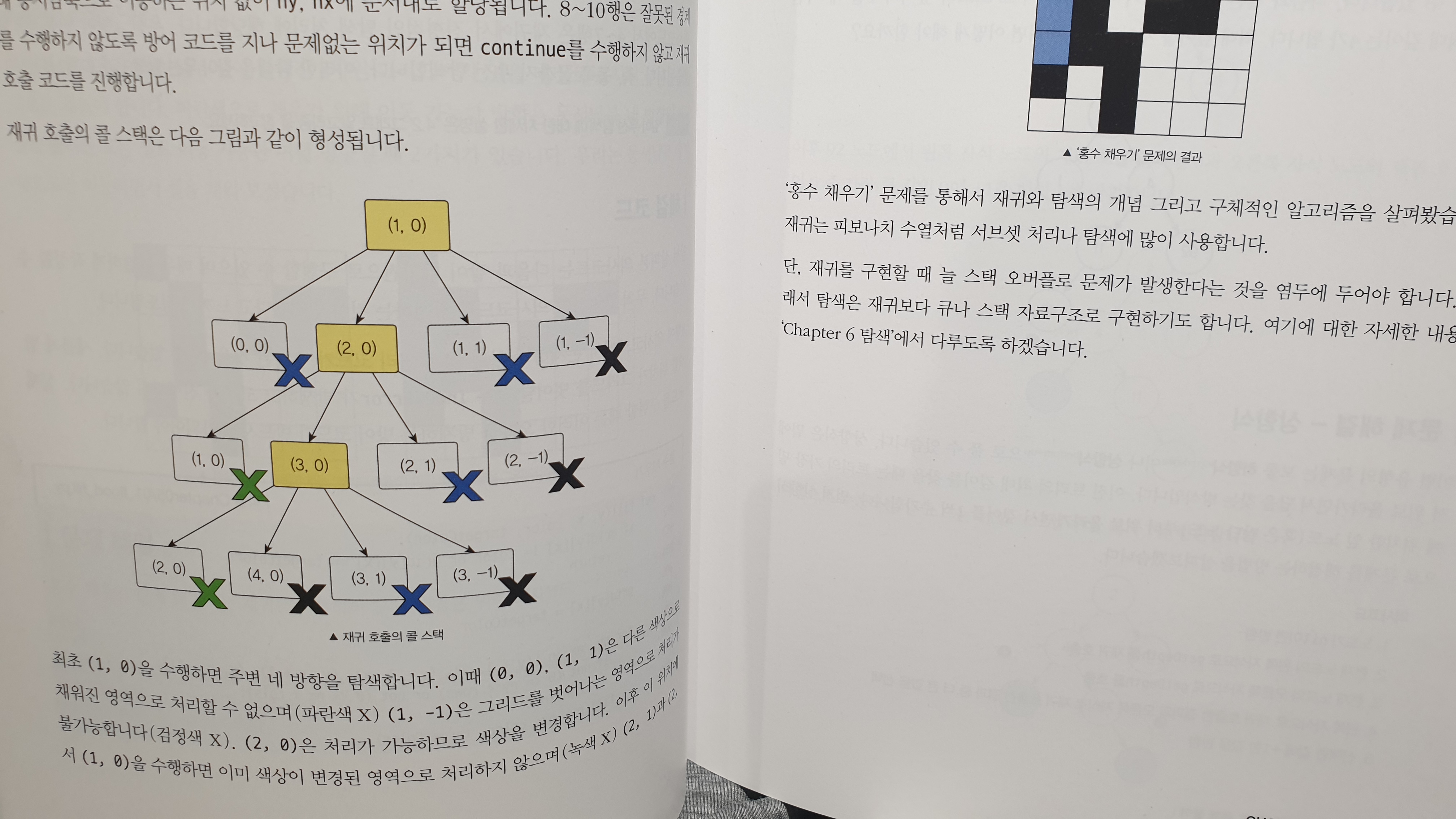
Chapter 5 재귀
재귀 알고리즘은 큰 문제를 작게 쪼개 해결하는 방법 중 하나로, 자기 자신(함수)를 호출한다는 특징 때문에 재귀라고 불립니다. 재귀가 핵심 알고리즘으로 손꼽히는 이유는 강력한 범용성 때문입니다. 탐색 알고리즘에서도 재귀가 쓰입니다. 재귀 알고리즘 개념은 간단하지만 명확한 이해 없이 제대로 구현하는 것이 그리 쉽지 않습니다.
Chapter 6 탐색
넓은 2차원 행렬에서 최단 거리를 찾거나 장애물을 피하면서 유일한 출구를 찾을 때는 행렬의 크기, 장애물의 위치, 출구의 위치 등이 테스트 케이스마다 다르게 입력되기 때문에 경우의 수가 무척 많습니다. 이렇게 일일이 코딩하는 것이 무척 비효율적일 때는 발생 가능한 모든 경로를 수행하면서, 즉 탐색하면서 문제를 해결할 수 있는지 없는지를 판단해야 합니다.
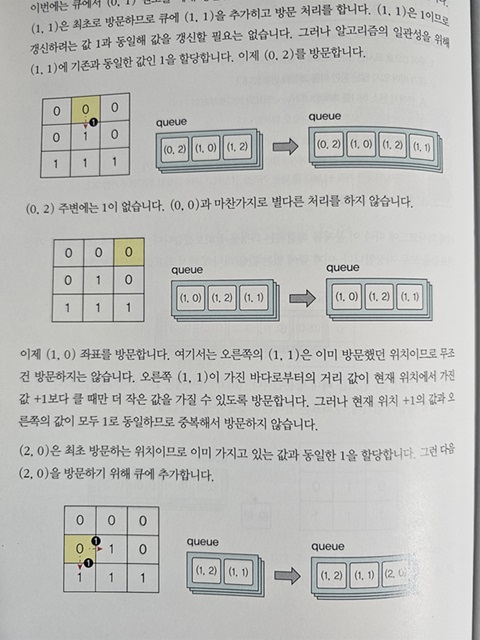
탐색 문제 해결 방법은 2가지가 있습니다. 첫 번째는 재귀 방식으로 방문 가능한 모두 방문하는 것이고, 두 번째는 큐 혹은 스택 자료구조를 사용해 모든 경로를 탐색하는 것입니다.
Chapter 7 공간
알고리즘 문제 중에는 기하하적인 특징을 파악해서 풀어야 하는 문제들이 있습니다. 불규칙하게 분포되어 있는 항목들을 균등하게 분포하는 방법을 찾는 문제라든가, 위치별로 서로 다른 특성을 가지고 있는지를 찾아내야 하는 문제, 공간에 배치된 숫자들을 순회 규칙에 따라서 방문해야 하는 문제 등 공간이 특징을 파악해야 해결이 가능한 문제들이 있습니다.
Chapter 8 순열과 조합
확률과 통계에서 가장 먼저 짚고 넘어가야 하는 것은 확률과 통계의 정의입니다. 통계란, 조사하고자 하는 전체 집단(모집단)의 일부(표본)를 획득해 평균, 분산 등 다양한 수치를 산출하는 것을 뜻하고, 확률이란 경우의 수 중 특정 사건이 발생할 가능성을 뜻합니다. 특히 확률에서는 경우의 수를 아는 것이 무척 중요한데요. 이때 발생 가능한 경우의 수를 모은 집합을 표본 공간이라 합니다. 이런 발생 가능한 모든 경우의 수를 찾는 문제 혹은 모든 조합을 찾는 알고리즘 문제들은 가장 자주 접하는 문제 유형 중 하나로, 이번 장에서는 이와 관련된 몇 가지 문제들을 살펴봅니다.
Chapter 9 배열
특정 구간에 겹치지 않는 시간을 찾거나 여러 거래 내역에서 유효하지 않는 거래를 찾는 등 문제 상황에 배열이 주어지는 유형의 알고리즘을 살펴봅니다. 배열 유형이지만 해결에 다양한 알고리즘을 사용할 수 있습니다. 단, 배열 유형은 일관된 패턴이 존재하지 않기 때문에 이론부터 학습하는 것보다 문제를 직접 살펴보면서 빠르게 해결 방법을 알아보겠습니다.
Chapter 10 정렬
대부분 정렬 문제의 목적은 주어진 값을 오름차순 혹은 내림차순으로 배치하는 것입니다. 단순히 주어진 숫자들을 오름차순 혹은 내림차순으로 정렬하는 문제만 존재한다면 우리가 흔히 알고 있는 퀵 정렬, 머지 정렬과 같은 알고리즘만 파악하고 있으면 됩니다. 그러나 문자열의 출현 빈도에 따른 정렬이라든지, 행렬 내 대각선 방향으로 원소들을 정렬해야 하는 등 정렬을 하는 다양한 규칙이 주어지고 이 규칙을 만족하는 알고리즘을 찾아야 하는 문제들이 있습니다.
Chapter 11 검색
검색은 복잡한 알고리즘을 풀어나갈 때 필요한 가장 기본적인 알고리즘으로, 입력으로 주어진 배열에서 특정 값을 찾는 문제에 흔히 쓰입니다. 또, 검색 알고리즘은 다른 복자한 알고리즘을 해결하는 데 부품처럼 사용되기도 하므로 같은 검색 기능을 제공해도 보다 빠르게 검색할 수 있는 효율적인 알고리즘을 구현하는 것이 중요합니다.
Chapter 12 문자열
문자열 분리, 분석, 문자 변환 및 검사 등을 다루면서 문자열에 관한 문제 유형을 살펴보겠습니다. 앞뒤로 똑같이 읽히는 팰린드롬, 문자를 재배치하여 다른 단어를 만들어내는 애너그램, 문자열을 빠르게 찾기 위한 롤링해서 윈도우 등 문자열과 관련된 문제들은 특성에 맞는 적합한 방법을 찾아서 해결해야 합니다.
PART 04 알고리즘별 문제 풀이 II
이론과 실전을 한번에 손에 익히기 위한 이론과 문제 풀이를 다루며, 이전에 학습한 트리, 그래프, 기본 자료구조에서 좀 더 심화된 개념을 살펴보고 다양한 문제를 풀어봅니다.
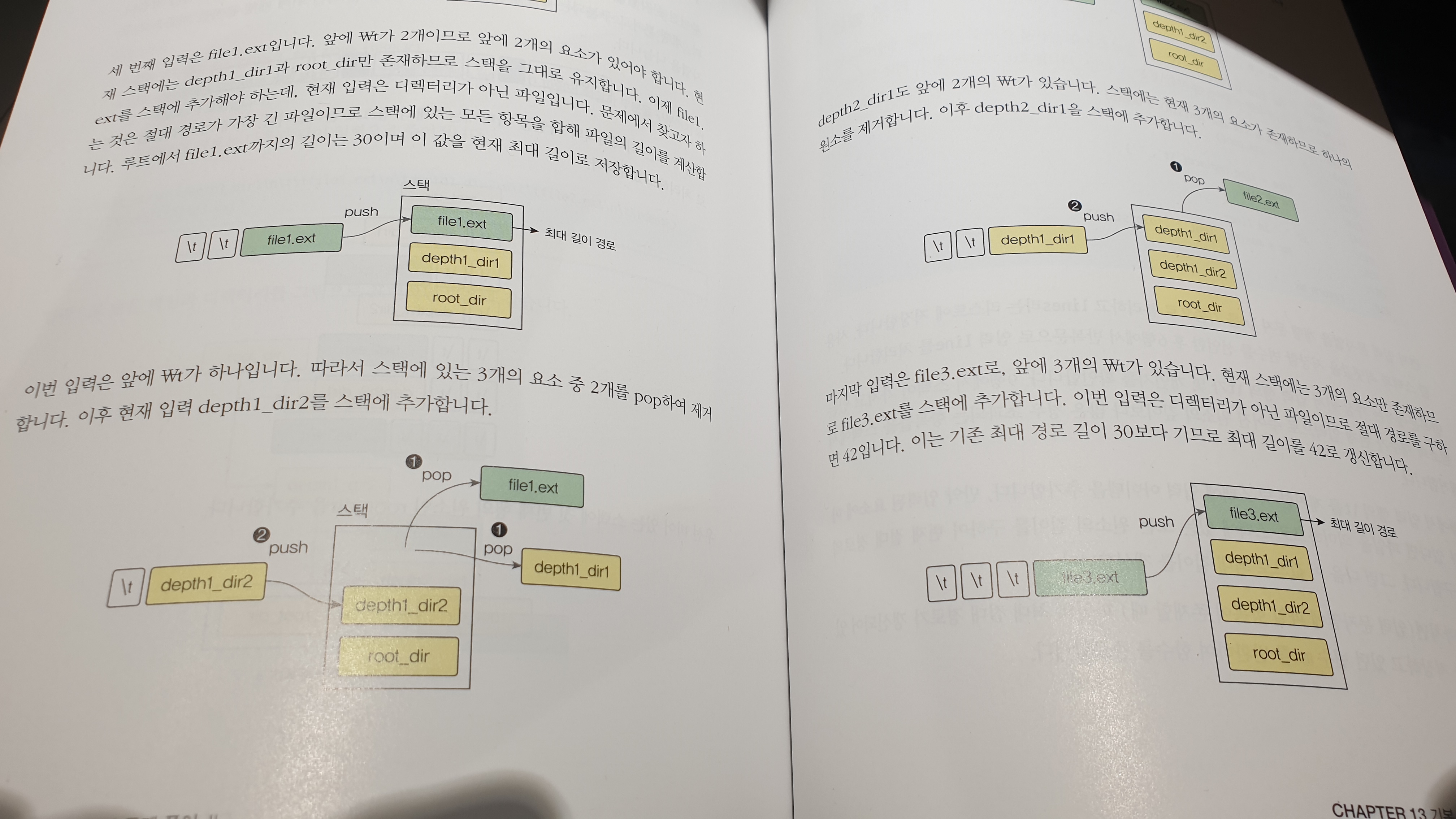
Chapter 13 기본 자료구조 활용
스택, 리스트 등 여러 자료구조를 활용해 풀 수 있는 문제들을 살펴봅니다. 경로가 가장 긴 파일명을 찾으면서 스택을 활용하고 입력된 여러 정수를 특정한 크기로 분할하며 리스트를 다루는 것은 물론 헬퍼 함수와 제한된 시간 안에 성능을 비약적으로 높이는 방안까지 살펴보겠습니다. 문제 풀이 과정을 통해 자료 구조를 잘 사용하는 것이 얼마나 중요한지 알 수 있습니다.
Chapter 14 트리
기본적인 순회부터 트리의 깊이와 모든 경로 파악하기 등 트리 알고리즘에서 학습했던 내용을 응용해서 풀 수 있는 몇 가지 문제를 살펴봅니다.
Chapter 15 그래프
가장 연결이 많은 정점 찾기, 최소 비용으로 모든 정점 순회화기, 사이클 여부 확인하기 등 그래프 알고리즘을 응용해서 해결할 수 있는 문제들에 대해 살펴봅니다.
Chapter 16 숫자
숨겨진 수열 찾기, 최댓값 리스트 생성하기, 주어진 목표 값으로 나눌 수 있는 쌍의 개수 찾기, 총합이 특정 값인 부분 집합 찾기 등 여러 숫자 사이에 숨겨진 관계를 파악하여 풀어야 하는 문제 유형을 다룹니다. 곱셉, 나눗셈, 누적, 감소 등 각 숫자에 적용된 다양한 규칙을 찾아 풀면서 값들의 관계를 파악하는 훈련을 합니다.
Chapter 17 동적 계획법
동적 계획법이란, 직전까지의 단계를 수행해서 얻은 결과를 재사용하여 현재의 해를 찾으며 이를 프로그래밍 방식으로 구현할 때 동적으로 해의 테이블을 프로그래밍한다는 의미를 가지고 있습니다. 분할 정복과 유사하나 해결된 부분의 해를 집합에 넣고 이를 재사용하여 같은 부분 문제는 다시 연산하지 않는다는 점에서 다릅니다.
동적 계획법을 문제 풀이에 적용하려면 문제는 최적의 부분 구조여야 합니다. 이 말은 부분 문제는 2개 이상의 문제를 푸는 데 사용됨을 의미합니다. 이는 큰 해는 작은 최적해의 합을 의미합니다. 또, 중복되는 부분 문제여야 하며 답을 한 번만 계산하고 이를 재활용할 수 있는 구조여야 합니다. 동적 계획법을 적용하는 방법은 크게 2가지로, 하양식과 상향식입니다.
책의 총평
코딩 공부를 하고 싶은 사람에게 알고리즘 기본기부터 개념을 쌓을 수 있는 아주 좋은 책으로, 향후 개발을 함에 있어 확실히 도움이 될 것으로 보입니다. 그러나 내용이 너무 반복적으로 알고리즘 설명만 얘기를 하고 있어, 처음 도전하는 사람에게는 어려울 수 있습니다. 총 86개의 알고리즘 예시가 있는데, 이를 도서만 보면서 접근시 자칫 혼란을 줄 소지가 있어 보입니다. 저도 처음에는 도서에 나온 예시만 보고 하다 추후 깃 소스를 내려받아 확인하면서 다시 보니 내용이 상이한 부분이 더러 있습니다. 향후에는 완성도를 높이기 위해 깃 소스와 도서가 일치하면 좋을 거 같습니다.
한빛미디어 <나는 리뷰어다> 활동을 위해서 책을 제공받아 작성된 서평입니다.